Плетіння кіс – хіба це математика?
Плетіння кіс – хіба це математика 👩🦰💇♀️? Часто вважають, що математика вивчає абстрактні поняття, а такий предмет побуту як коса до математики не має жодного відношення.
Але це не так. Сьогодні математики займаються не лише серйозними та глибокими, піднесеними над повсякденністю проблемами, такими як теорія чисел, розрахунки космічних польотів, а й більш земними питаннями. Зокрема, теорією кіс та пов’язаною з нею теорією вузлів.
👉 Це реальна і жива наука, що виникла в 20-х роках минулого сторіччя і ще не завершена і не вичерпала свого застосування. А за красою теорія кіс та вузлів не поступається класичній, але застиглій у своїй величі математиці античності та ХVІ–ХVII століть, яку вивчають у школі.
⭐Вузли та коси – предмети прості та наочні. Ви, звичайно, зустрічалися з ними у повсякденному житті, але, можливо, не підозрювали, що це ще й математичні об’єкти. Більше того, останні 30 років математики та фізики з величезним інтересом та дивовижною інтенсивністю почали займатися відповідними теоріями. Досить зауважити, що чотири медалі Філдса (ця медаль вважається найвищою нагородою в математиці!) були отримані саме за роботи, пов’язані з цією теорією кіс та вузлів. Лауреатами премії Філдса в різні роки стали Володимир Дрінфельд із Харкова (робота в Чикаго), Воган Джонс із Нової Зеландії (робота у Каліфорнії), Едвард Віттен (робота у Прінстоні).
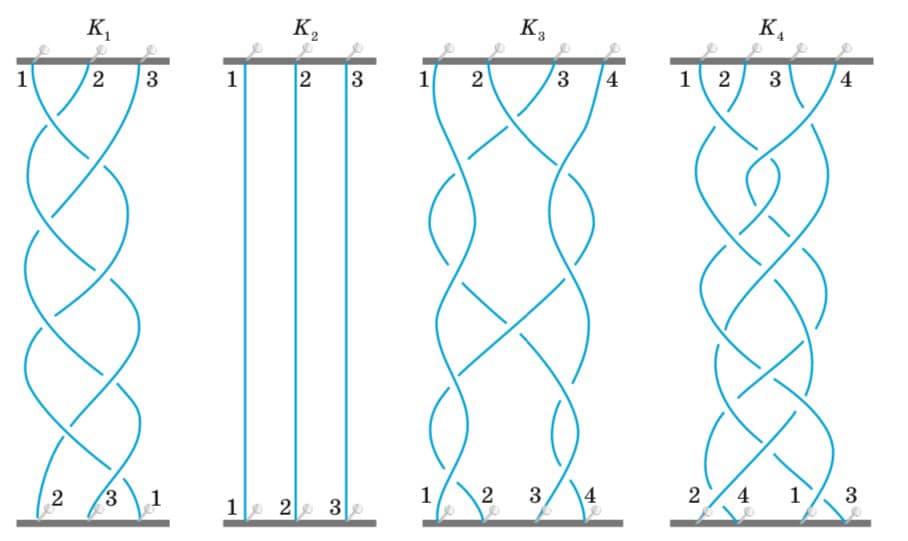
Розглянемо поняття коси 😉. Математична коса складається з n ниток (тобто кривих у просторі), які починаються в n точках горизонтальної прямої і закінчуються в n точках іншої горизонтальної прямої, розташованої нижче. При цьому нитки мають бути низхідними, тобто дотичний вектор у будь-якій точці кривої повинен весь час «дивитися вниз», йому заборонено бути горизонтальним і тим більше «дивитися вгору».
Косу можна уявляти так: у верхній і нижній краї вертикальної дошки вбито по n гвіздків (n може дорівнювати 1, 2, 3, …), і кожен із гвіздків верхньої основи з’єднаний ниткою з одним із гвіздків нижньої; нитки попарно не перетинаються і повинні опускатися вниз.
😍 Коси – це один із найпростіших геометричних об’єктів, які легко піддаються «алгебраїзації»: до кіс із однаковим числом ниток можна застосовувати дію множення, при цьому отримують алгебраїчний об’єкт, який називають групою кіс з n ниток. Він не дуже простий, але ґрунтовно вивчений. 🙂
Для тих, кому краса не є достатньою підставою для вивчення предмета, зауважимо, що відповідь на запитання «Навіщо це все потрібно?» міститься в самій історії виникнення теорії кіс.
Теорія кіс була створена у 20-х роках минулого століття тоді ще молодим німецьким алгебраїстом Е. Артіном при виконанні замовлення… ткацької фабрики. Тобто можна сказати, що він виконував виробниче завдання.
⚡ Сьогодні теорія кіс – це теорія, що пов’язує воєдино перестановки та многочлени без кратних коренів, це об’єднання алгебри, геометрії та топології. Крім того, завдяки рівнянням Янга-Бакстера коси пов’язані з фізикою, а останніми роками – з найновішим напрямком, що лежить на стику кількох наук, – квантовими комп’ютерами.